class: center, middle, inverse, title-slide # Introducción al análisis de datos biológicos con R ## Clase 3 ### <img src = 'https://github.com/Soma-dos-Quadrados/ArtesSoma/blob/main/simbolo_smfundo4.png?raw=true' width = '25%'> ### Eliana F. Burgos --- #Contenidos <br> 1.[Variables estadísticas](#vestad) 2.[Distribución de probabilidaes](#distrib) 3.[Estadística descriptiva: medidas de posición](#posicion) 4.[Estadistica descriptiva: medidas de dispersión](#dispersion) 5.[Ejercicios](#ejercicios) <center>  --- class: inverse, center, middle # Variables estadísticas --- ##**Variables estadísticas** **Elementos de la población -> unidades estadísticas** 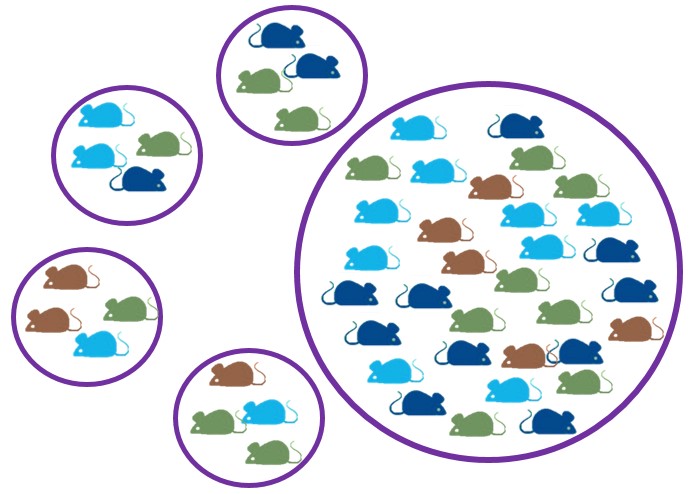 --- ##**Variables estadísticas** <br> - **Variables cualitativas ** - *ordinales* - *nominales* - **Variables cuantitativas** - *discretas* - *continuas* <center> 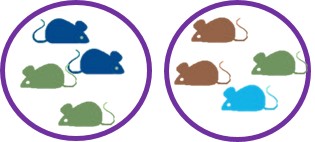 --- ##**Variables estadísticas** - **Variables cualitativas ** - *ordinales* **->** tamaño (grande, mediano, pequeño); distancia (muy lejos, lejos, cerca); clases de edades; año de muestreo; tratamiento (1,2,3;a,b,c) - *nominales* **->** sexo, especie, sitio, color, uso del suelo, cuadrante, presencia/ausencia - **Variables cuantitativas** - *discretas* **->** abundancia, indv. positivos, cantidad de huevos/embriones - *continuas* **->** índices, peso, largo, temperatura, humedad, intensidad luminica <center>  --- ##**Ejemplo** ><img src = 'paper_Sanchez_ejemplo.jpg' width = '65%'> **OBJETIVO**: evaluar la dieta y el nicho dietario de especies de murciélagos frugívoros. <br> <center> <img src = 'murcis.jpg' width = '65%'> --- ##**Ejemplo** **METODOLOGíA** **Datos**: recopilaron datos novedosos y utilizaron datos de estudios previos - **Murcielagos** - masa corporal - largo del antebrazo - sexo (macho, hembra) - edad (juvenil, adulto) - **Vegetación**: colectaron ejemplares en cada sitio - tamaño individual de las semillas - color de la fruta - forma de la fruta - n° de semillas por fruto - habitat (bosque primario vs bosque secundario ribereño) ---  <br> Parámetro | Tipo de variable ------------- | ------------- **Murcielagos**| masa corporal| cuantitativa continua largo del antebrazo| cuantitativa continua sexo | cualitativa nominal de dos niveles: macho/hembra edad | cualitativa ordinal de dos niveles: juvenil/adulto ---  Parámetro | Tipo de variable ------------- | ------------- **Vegetación**| tamaño de semilla| cuantitativa continua color del fruto|cualitativa nominal forma del fruto|cualitativa nominal n° de semillas por fruto| cuantitativa discreta habitat| cualitativa nominal de dos niveles: bosque primario/bosque secundario --- ##**Ejemplo** ><img src = 'lonomias.jpg' width = '85%'> <br> **OBJETIVO**: analizar el perfil eco-epidemiológico de accidentes y ocurrencias de taturanas (*Lonomias sp*) en Misiones (Argentina) entre enero de 2014 y mayo de 2020 --- **Ejemplo** **METODOLOGíA** **Datos**: epidemiológicos y registros a campo - **Accidentes** - aspectos socio-demográficos - localidad del accidente - hora del día - circunstancias del accidente - área anatómica afectada --- **Ejemplo** **METODOLOGíA** - **Ocurrencia** - planta hospedadora - tipo de ambiente - **Nicho ecologico de las taturanas** - Temperaturas máximas y mínimas - Precipitaciones - Evapotranspiración --- <img src = 'lonomia.jpg' width = '50'> <br> Parámetro | Tipo de variable ------------- | ------------- **Accidentes** | sexo | cualitativa nominal de dos niveles: m/f grupo etario| cualitativa ordinal de 7 niveles: 0-10; 11-20; 21-30; 31-40; 41-50; 51-60; 61-70 hora del día| cualitativa ordinal de tres niveles: 6-12; 12:01-18:00; desconocido circunstancias del accidente| cualitativa nominal de tres niveles: duramte el trabajo; durante recreación; desconocido área anatómica afectada| cualitativa nominal de tres niveles: miembros inferiores; miembros superiores; tronco --- <img src = 'lonomia.jpg' width = '50'> <br> Parámetro | Tipo de variable ------------- | ------------- **Ocurrencia**| Planta hospedadora| cualitativa nominal Tipo de ambiente| cualitativa nominal de cuatro niveles: urbano, periurbano, rural, bosque **Nicho**| Temperaturas máx y min| cuantitativa continua Precipitaciones| cuantitativa continua Evapotrasnpiracion| cuantitativa continua --- ###**IMPORTANTE** <br> Cuando cargamos la planilla al R, el programa lee cada columna con la categoria asignada en el procesador de bases de datos No siempre esa categoria es la correcta y hay que configurarla ``` ## ## -- Column specification ---------------------------------------------------------- ## cols( ## .default = col_double(), ## fecha = col_character(), ## sitio = col_character(), ## uso_suelo = col_character(), ## ambiente = col_character(), ## estacion = col_character(), ## anio.estacion = col_character() ## ) ## i Use `spec()` for the full column specifications. ``` --- **Entonces** ***variable cualitativa*** ```r class(datos$uso_suelo) ``` ``` ## [1] "character" ``` ```r datos$uso_suelo <- as.factor(datos$uso_suelo) class(datos$uso_suelo) ``` ``` ## [1] "factor" ``` --- <br> <br> ***variable numérica continua*** ```r datos$IDR_total <- as.numeric(datos$IDR_total) class(datos$IDR_total) ``` ``` ## [1] "numeric" ``` ***variable numérica discreta*** ```r class(datos$n_total) ``` ``` ## [1] "numeric" ``` ```r datos$n_total <- as.integer(datos$n_total) ``` --- ##**Distribución de probabilidades** - **función** - asigna a cada suceso definido sobre la variable la probabilidad de que dicho suceso ocurra. - está definida sobre el conjunto de todos los sucesos y cada uno de los sucesos es el rango de valores de la **variable aleatoria** - tiene una relación estrecha con las distribuciones de frecuencia, ya que describe **cómo se espera** que **varíen** los resultados  --- <br> <br> Distribución | Alias --------------------------- | ---------------- Distribución normal | norm Distribución Binomian | binom Distribución de Poisson | pois Distribución exponencial | exp Distribución t de Student | t Distribución Chi cuadrao | chisq Distribución F | f <img src= 'https://ih1.redbubble.net/image.1408993388.8256/st,small,507x507-pad,600x600,f8f8f8.jpg' width=15%> --- <br> <br> Funciones | Sintaxis |Explicacion --------------| ----------------|-------------- densidad | dnorm | devuelve el valor de la función de densidad de probabilidad | dbinom | probabilidad de obtener un determinado número de aciertos en un determinado número de ensayos | dpois | probabilidad puntual para un determinado valor probabilidad |pnorm | |pbinom |probabilidad de que la variable tome valores menores o iguales que *x* | ppois | cuantiles | qnorm | |qbinom |permite encontrar el cuantil (percentil) para cualquier probabilidad *p* | qpois | --- ##**Distribucion normal** <img src= 'normal.jpg' width=15%> - es una de las distribuciones de probabilidad de variable continua más frecuente - permite modelar numerosos fenómenos naturales, sociales y psicológicos - está identificada por una combinación de valores de dos parámetros: `\(\mu\)` y `\(\sigma\)` - definida por una **Función de densidad** <center> 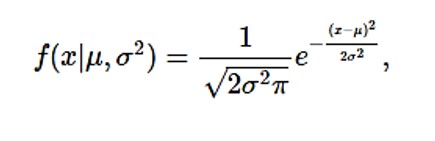 `\(\mu\)` = media, mediana y la moda de la distribución `\(\sigma\)` = la desviación estándar ( `\(\sigma\)` >0 ) `\(\sigma^{2}\)` = la variación Estandarizar->***N*** **( `\(\mu\)` , `\(\sigma\)`)** **->** ***N*** **(0,1)** --- ###**Distribucion normal** <br> ```r library(stats) help("Distributions") ``` Vamos a modelar una distribución normal ```r hist(y, breaks = 40, freq = FALSE, main="") lines(density(y), lwd = 2, lty=3, col="darkgrey") xvec <- seq(min(y)-0.5,max(y)+0.5, by=0.1) lines(xvec, dnorm(xvec, mean = mu, sd = sigma), lwd = 2) ``` <!-- --> --- ##**Ejemplo** <br> Estamos estudiando el proceso de invasión de árboles en la sabana del Parque Nacional El Palmar, y para eso desarrollamos un experimento en el que colocamos plántulas de *Allophylus edulis* cerca de las palmeras y medimos su altura al cabo de un año. Sabemos que la media de la altura de esta especie es de 8 cm y la varianza es de 6.25 cm. <!-- --> --- <br> <br> Sabemos que nuestra variable altura tiene una distribución normal. Si la plantula logra pasar la altura media en cercania de una palmera, tiene mayor probabilidad de asentarse y queremos evaluar qué probabilidad hay de que la plántula crezca por debajo de la media+su desvio estandar ( es decir, por debajo de 8-2.5= 5.5) al cabo de un año de comenzado el experimento. ```r pnorm(5.5, mean=8, sd=2.5) ``` ``` ## [1] 0.1586553 ``` ```r pnorm(12, mean=8, sd=2.5) ``` ``` ## [1] 0.9452007 ``` ```r qnorm(0.9452007, mean=8, sd=2.5, lower.tail = FALSE) ``` ``` ## [1] 4 ``` --- ##**Distribucion Binomial** <img src= 'paranormal.jpg' width=20%> - una distribución de probabilidad de una variable discreta. - Describe el resultado de ensayos independientes de ***n*** - puede generar dos resultados: - positivo vs. negativo; presente vs ausente -> **Bernoulli** - cantidad de positivos vs. cantidad de examinados -> **Binomial** - la variable toma valores discretos cuya probabilidad depende de ***n***, definido como el número de ensayos, y ***p***, definido como la probabilidad del resultado a contar en cada ensayo. <center> <img src= 'funcion_binomial.jpg' width=75%> --- ##**Ejemplo** <br> Además de ver que tanto crecieron las plántulas de *A. edulis* queremos saber también cuántas sobrevivieron en un año. - Entonces, si instalamos 5 plantulas por parcela, en un total de 5 parcelas, nuestro ***n*** = 25. - Sabemos por estudios previos que la probabilidad de que una plantula al azar colocada cerca de una palmera sobreviva es de ***p***= 0.3 - Queremos saber cual es la probabilidad de que ninguna sobreviva ```r p <- 0.3 n <- 25 k <- 0 dbinom(k,size=n,prob=p) ``` ``` ## [1] 0.0001341069 ``` --- <br> <br> ```r n <- 0:25 plot(dbinom(n, size = 25, prob = 0.3), type = "h", lwd = 2, main = "Función de probabilidad binomial", ylab = "P(X = x)", xlab = "Número de éxitos") ``` <!-- --> --- <!-- --> --- <br> - Tambien podemos calcular la probabilidad con la siguiente funcion ```r pbinom(n,25,0.3) ``` ``` ## [1] 0.0001341069 0.0015709661 0.0089605279 0.0332405166 0.0904719186 0.1934884421 ## [7] 0.3406549043 0.5118485440 0.6769281251 0.8105639765 0.9021999889 0.9557535026 ## [13] 0.9825302595 0.9940060124 0.9982215951 0.9995464926 0.9999013758 0.9999818955 ## [19] 0.9999972326 0.9999996543 0.9999999656 0.9999999974 0.9999999999 1.0000000000 ## [25] 1.0000000000 1.0000000000 ``` ```r plot(pbinom(n, size=25, p=0.3)) ``` <!-- --> --- Comparamos dbinom | pbinom --------- | --------- 0.000134 | 0.99986 ¿Cuál es la diferencia? **dbinom** expresa la función de masa, es decir la función de probabilidad; muestra la probabilidad de tomar al azar una plantula que no sobrevivió **pbinom** expresa la funcion de distribución acumulada; muestra la probablidad de supervivencia en las plantas ``` ## [1] 0.1934884 ``` ``` ## [1] 0.5118485 ``` Ademas tenemos la funcion **qbinom** para conocer los cuantiles (devuelve la función de densidad acumulativa inversa): ```r qbinom(p = 0.511848, size = 25, prob = 0.3) ``` ``` ## [1] 7 ``` --- ##**Distribucion Bernoulli** <img src= 'paranormal.jpg' width=20%> - toma valores de 0 y 1 ```r bb <- rbinom(25,size=1,prob=0.3) bb ``` ``` ## [1] 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 1 0 0 0 ``` --- <!-- --><!-- --> <!-- --><!-- --> --- ##**Distribución de Poisson** <img src= 'paranormal.jpg' width=20%> <br> - es una distribución de probabilidad discreta - se usa en conteos - La ocurrencia media por intervalo suele representarse con la letra griega lambda `\(\lambda\)` y, en base a dicho valor, la distribución de Poisson estima la probabilidad de que se produzcan *x* sucesos dentro de un intervalo dado <center> <img src= 'poisson_distri.jpg' width=75%> --- ##**Ejemplo** - Siguiendo con el ejemplo anterior, cuantas plantulas crecieron al lado de las palmeras despues de un año ```r dpois(0, lambda = 5)#probabilidad de que ninguna crezca ``` ``` ## [1] 0.006737947 ``` ```r dpois(12, lambda =5)#probabilidad de que crezcan 12 ``` ``` ## [1] 0.00343424 ``` ```r ppois(1, lambda = 5) #probabilidad de que mas de una sobreviva ``` ``` ## [1] 0.04042768 ``` ```r ppois(25, lambda = 5)#probabilidad de que sobrevivan todas ``` ``` ## [1] 1 ``` ```r p <- c(0.25, 0.50, 0.75) qpois(p, lambda = 5) ``` ``` ## [1] 3 5 6 ``` --- <br> <br> <br> <center>  --- #**Estadistica descriptiva** <br> - *descripción de una población* - descripción de las diferentes variables - teniendo en cuenta: - valor medio - dispersión/variación - forma --- ###**Medidas de posición** <br> - son medidas de tendencia central - marcan la acumulación de los datos en torno a un valor - **media, mediana y moda** ###**Media** - muestra el valor promedio de nuestra variable de interés <center> <img src= 'media.jpg' width=30%> --- <br> <br> Podemos calcular la media para nuestra muestra completa o definir qué valores queremos excluir del cálculo **Ejemplo** La especie *Steindachneridion melanodermatum*, conocido como "surubí del Iguazú" es una especie endémica de la cuenca del río Iguazú. Queremos saber cual es el peso promedio de la población que estamos estudiando --- <img src= 'http://www.ecoregistros.org/site/images/dataimages/2018/08/27/283544/FB_IMG_1535301136111.jpg' width=10%> **Media de toda la muestra** ```r mean(surubi$peso) ``` ``` ## [1] 3.668524 ``` **Media de un conjunto de datos recortado** ```r mean(surubi$peso, na.rm = TRUE, trim = 0.025) ``` ``` ## [1] 3.636535 ``` El comando *trim()* nos permite indicar los datos que queremos excluir de cada extremo de la distribución --- <br> <br> - Si además de los datos que tomamos en campo, contamos con estudios previos y queremos conocer la media de esa población utilizando todos los datos, se puede calcular la media ponderada - Esto se realiza con una adaptación de la formula donde incluimos la media y en *n* de las bases que vamos a utilizar. Por ejemplo: nuestros datos tienen una media de 3.668 kg (*n*=50), y los estudios previos muestran medias de 2.15 kg (*n*=25), 3.12 kg (*n*=47) ```r mpond <- ((3.668*50)+(2.15*25)+(3.21*47))/(50+25+47) mpond ``` ``` ## [1] 3.180492 ``` --- ##**Mediana** <br> - es el valor que se encuentra en la mitad en la lista ordenada de nuestros datos ```r median(surubi$peso) ``` ``` ## [1] 3.583357 ``` ##**Moda** - la moda es el valor más frecuente en nuestros datos - se puede programar siguiendo ```r frecuencias <- data.frame(table(surubi$peso)) moda <- frecuencias[which.max(frecuencias$Freq),1] moda ``` ``` ## [1] 3.583357449 ## 33 Levels: 1.53907058 1.820126645 1.884465124 2.069217919 ... 7.33345747 ``` --- <br> <br> ```r library(modeest) mfv(surubi$peso) ``` ``` ## [1] 3.583357 ``` --- #**Estadistica descriptiva** ##**Medidas de dispersión** - nos permiten visualizar que tan variables o dispersos son nuestros datos - valores mínimos y máximos, varianza, el desvío estandar, asimetria y curtosis, cuantiles ##**Mínimo y máximo** ```r min(surubi$peso) ``` ``` ## [1] 1.539071 ``` ```r max(surubi$peso) ``` ``` ## [1] 7.333457 ``` ```r range(surubi$peso) ``` ``` ## [1] 1.539071 7.333457 ``` --- ##**Varianza** - es el promedio de los cuadrados de los desvíos - Es la esperanza del cuadrado de la desviación típica de dicha variable respecto a su media - se expresa en la unidad de la variable al cuadrado <center> <img src= 'varianza.jpg' width=40%> ```r var(surubi$peso) ``` ``` ## [1] 1.837311 ``` --- <br> ##**Desvio estandar** - es la raíz cuadrada de la varianza - se expresa en la misma unidad en la que estan nuestros datos <center> <img src= 'desvio.jpg' width=20%> ```r sd(surubi$peso) ``` ``` ## [1] 1.355475 ``` --- **Error estandar** - error estándar es la desviación estándar de la distribución muestral - una estimación de la desviación estándar, derivada de una muestra particular usada para computar la estimación. - es la desviación estándar dividida por la raíz cuadrada del número de observaciones. ```r library(plotrix) std.error(surubi$peso) ``` ``` ## [1] 0.1916931 ``` **Cálculo manual** - EE es el desvío estandar dividido la raíz cuadrada del n° de observaciones ```r sd(surubi$peso)/sqrt(length(surubi$peso)) ``` ``` ## [1] 0.1916931 ``` --- ##**Coeficiente de variación** - Comparar dos grupos de datos de forma estandarizada - permite comparar datos en diferentes escalas - a >CV, menor representatividad de la media - es una medida relativa **Datos que tomamos a campo** Masa corporal expresada en **kg** Teniamos una media de 3.67 kg con un desvío de 1.35 kg ```r sd(surubi$peso)/mean(surubi$peso)#(1.35/3.668) ``` ``` ## [1] 0.3694877 ``` **Datos de la bibliografía** Masa corporal expresada en **gr** Teniamos una media de 3120 gr (3.12 kg) con un desvio de 300 gr (0.30 kg) ```r (300/3120) ``` ``` ## [1] 0.09615385 ``` --- ##**Asimetria y curtosis** - dan cuenta de la forma general de los datos - nos permite identificar ciertas tendencias y comportamiento de los datos - se utilizan comandos de la librería **psych** **Asimetría** - da cuenta de cómo se organizan los datos alrededor de la media - pueden ser simétricas o asimétricas positivas o negativas - los valor deben encontrarse entre -2 y 2. ```r skew(surubi$peso) ``` ``` ## [1] 0.5488607 ``` nos devuelve un valor en la escala de la variable que no nos permite comparar entre diferentes set de datos, entonces lo podemos estandarizar ```r skew(surubi$peso)/sqrt(6/50) ``` ``` ## [1] 1.584424 ``` --- **Curtosis o apuntamiento** <br> - mide que tan apuntada o achatada es la distribución de los datos al cercanos a la media ```r kurtosi(surubi$peso) ``` ``` ## [1] -0.5993963 ``` ```r kurtosi(surubi$peso)/sqrt(6/50) ``` ``` ## [1] -1.730308 ``` **negativa** la distribución es **platicúrtica** **igual a cero** la distribución es **mesocúrtica** **positiva**la distribución es **leptocúrtica** En nuestro ejemplo, el peso de los surubí estudiados se distribuyen con una forma simétrica platicúrtica --- ###**¿Qué pasa si queremos comparar dos variables?** **Covarianza** - mide la asociación lineal entre dos variables - puede ser mayor, igual o menor que cero. - será positica cuando la variable respuesta aumente con el aumento de la explicativa - nos denota el tipo de relacion: positiva, negativa, neutra ```r cov(surubi$peso, surubi$largo) ``` ``` ## [1] 1.225165 ``` ```r cov(surubi$peso, surubi$temp) ``` ``` ## [1] 0.4468726 ``` --- **Correlacion** - nos permite estimar el grado en que estan correlacionadas dos variables - la relacion lineal será débil si el valor es cercano a cero - lineal directa fuerte si el valor es cercano a 1 - lineal inversa fuerte si es cercano a -1 ```r cor.test(surubi$largo, surubi$temp) ``` ``` ## ## Pearson's product-moment correlation ## ## data: surubi$largo and surubi$temp ## t = 1.0602, df = 48, p-value = 0.2943 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## -0.1326641 0.4122588 ## sample estimates: ## cor ## 0.1512695 ``` --- Con la libreria **GGally** <br> ```r ggpairs((surubi[,c(4:5)]), mapping=aes(color=surubi$sitio)) ``` <!-- --> --- ##**Cuartiles, deciles y percentiles** - se calcula con **quantile()** del paquete *stats* **cuartiles** ```r quantile(surubi$peso, prob=seq(0, 1, 1/4)) ``` ``` ## 0% 25% 50% 75% 100% ## 1.539071 2.343200 3.583357 4.689977 7.333457 ``` **Deciles** ```r quantile(surubi$peso, prob=seq(0, 1, length = 11)) ``` ``` ## 0% 10% 20% 30% 40% 50% 60% 70% 80% ## 1.539071 2.284228 2.334192 2.675262 3.414819 3.583357 3.583357 4.040215 5.226326 ## 90% 100% ## 5.527421 7.333457 ``` --- **Percentiles** <br> <br> ```r quantile(surubi$peso,seq(0, 1, length = 101)) ``` ``` ## 0% 1% 2% 3% 4% 5% 6% 7% 8% ## 1.539071 1.676788 1.814506 1.850366 1.881892 1.967604 2.058133 2.132954 2.205584 ## 9% 10% 11% 12% 13% 14% 15% 16% 17% ## 2.247867 2.284228 2.291649 2.291649 2.302450 2.316754 2.325514 2.332056 2.334192 ## 18% 19% 20% 21% 22% 23% 24% 25% 26% ## 2.334192 2.334192 2.334192 2.334192 2.334192 2.334192 2.334192 2.343200 2.360856 ## 27% 28% 29% 30% 31% 32% 33% 34% 35% ## 2.433705 2.568946 2.654938 2.675262 2.693952 2.710060 2.753246 2.847400 2.913087 ## 36% 37% 38% 39% 40% 41% 42% 43% 44% ## 2.914249 2.947201 3.068187 3.208360 3.414819 3.583357 3.583357 3.583357 3.583357 ## 45% 46% 47% 48% 49% 50% 51% 52% 53% ## 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 ## 54% 55% 56% 57% 58% 59% 60% 61% 62% ## 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 3.583357 ## 63% 64% 65% 66% 67% 68% 69% 70% 71% ## 3.583357 3.592402 3.604712 3.681899 3.787709 3.828474 3.834684 4.040215 4.371983 ## 72% 73% 74% 75% 76% 77% 78% 79% 80% ## 4.522504 4.537089 4.594564 4.689977 4.814564 4.969541 5.087930 5.161418 5.226326 ## 81% 82% 83% 84% 85% 86% 87% 88% 89% ## 5.278791 5.343644 5.429832 5.491607 5.503029 5.511189 5.511189 5.512575 5.518234 ## 90% 91% 92% 93% 94% 95% 96% 97% 98% ## 5.527421 5.550363 5.573119 5.594920 5.623100 5.697001 5.772370 5.864263 5.980026 ## 99% 100% ## 6.656742 7.333457 ``` --- ##**Algunos graficos descriptivos** **Grafico de cajas** <br> <br> ```r f1<- ggplot(surubi, aes(x= sitio, y= peso, fill=sitio))+ geom_boxplot() + xlab("peso") +theme (text = element_text(face= "bold" , size=15)) f1 ``` <!-- --> --- <br> <br> ```r f2<- ggplot(surubi, aes(x=peso, y=largo))+ geom_line()+ xlab("peso") + ylab ("largo") +theme (text = element_text(face= "bold" , size=15)) f2 ``` <!-- --> --- **Dudas y/o consultas** [efburgos@conicet.gov.ar]() ; [mariliabioufpr@gmail.com]() <center>  **Ejercicios** -> [Ejercicios.pdf]() **Formulario**-> [https://forms.gle/tmLsFUB5VfVqEcTKA]() *FIN*